第1308回-我家私塾-畢氏定理
從六月開始,我在家裡教兒子國中數學,六月底到國中報到後,接著暑假有比較多的時間可以陪伴他讀書。以往大多數的我家私塾時間,我都是在加強兒子比較弱的英語,但我覺得這樣兒子成就感很低,應該要來上一些他的強項-數學。
一開始是用姐姐的參考書,後來嘗試了洋蔥數學和均一,雖然很好用,但我總覺得玩數學應該是更有樂趣一些才對,我說的樂趣是指數學本身,不是指過關的獎賞。
前情提要:
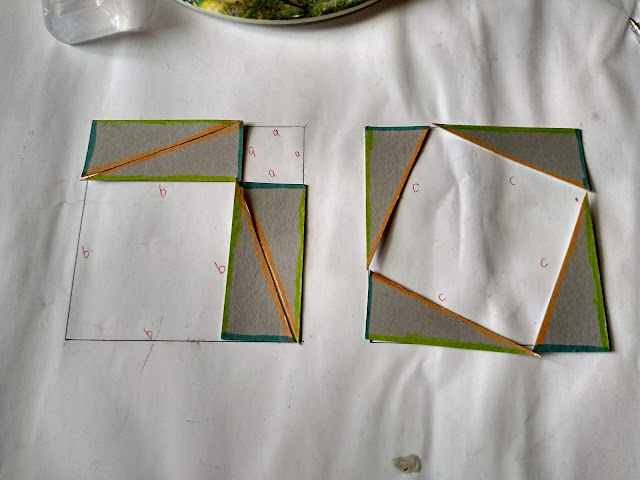
我先找網路上有關「畢氏定理」的資源,想想要怎麼用這些資源,我希望是用發現式的教學法來進行,而且不用管進度和時間壓力。
一開始是用姐姐的參考書,後來嘗試了洋蔥數學和均一,雖然很好用,但我總覺得玩數學應該是更有樂趣一些才對,我說的樂趣是指數學本身,不是指過關的獎賞。
前情提要:
- 第1287回-我家私塾-八的倍數判斷
- 第1289回-我家私塾-洋蔥數學-1-註冊帳號
- 第1290回-我家私塾-洋蔥數學-2-學生版與教師版體驗
- 第1291回-我家私塾-均一教育平台-1
- 第1292回-我家私塾-均一教育平台-2-教師後台
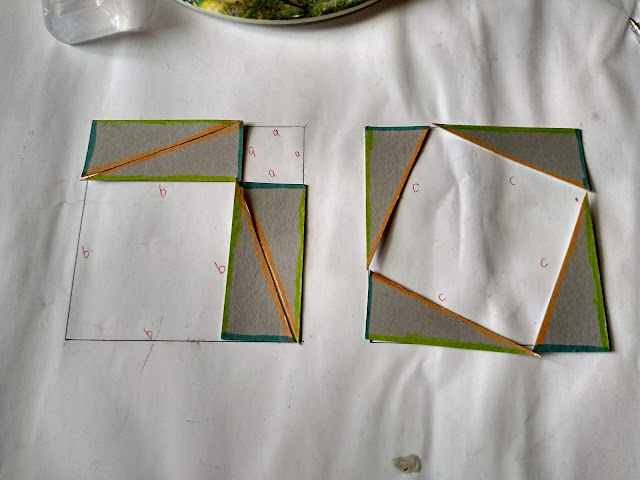
我先找網路上有關「畢氏定理」的資源,想想要怎麼用這些資源,我希望是用發現式的教學法來進行,而且不用管進度和時間壓力。
- Pythagorean theorem water demo - YouTube 直接給孩子看,不先解釋要做什麼,保有最珍貴的第一次體驗,這要是被說破了A平方+B平方=C平方就沒價值了
- 畢氏定理的引入 | 畢氏定理 | 均一教育平台 洋蔥數學, 商高,勾股弦定理,345 可操作看看蠻有趣的,3800年前,巴比倫人,2600年前印度,希臘畢氏定理,歐幾里德。有四百多個證明方法。畢氏定理連結了幾何學和代數,是橋樑。
- 巧手摺紙學數學--摺紙證明畢氏定理(方法2) - YouTube 這個我最愛!
- 數學家的故事---畢達哥拉斯 - YouTube 卡通 康軒國中數學 數學家---畢達哥拉斯的故事
- 商高定理及應用Ⅰ - YouTube
- 愛因斯坦聰明證明畢氏定理 - YouTube
7/22 我們是先從平方出發,先分別寫出1到13的平方是多少,然後我要兒子找找看,有哪些數的平方,可以變成兩個數的平方相加?兒子大約花三分鐘就找出 3-4-5,而且他還發現可以無限的寫下去,有倍數關係就可以一直寫。我說再找找沒有倍數關係的組合,大約花了七分鐘,他又找到 5-12-13的組合。過程中我一度想提示,但他說他的找法和我不一樣,不想聽我講,這也很好,我是用加法他是用減法,都可以的。
我在看過畢氏定理的引入 | 畢氏定理 | 均一教育平台 後,覺得「畢氏定理」作為代數和幾何的橋樑,非常適合做為在我家私塾時間探索的開頭。我跟兒子說「平方」讓人想到的第一件事情就是正方形面積,我要兒子剪三個正方形。
做好之後,兒子很自然地就把三個正方形排成上圖的樣子,我很驚訝地問他為什麼要這樣排?他笑說之前他有看到我在看數學影片時,我叫他不要看我要鋪梗,雖然他只看了一眼但已經記住那個排法了。哈哈,本來是要給他看倒水的影片,後來忘記給他看了。
我問兒子說你覺得那三個正方形圍起來的三角形,會不會是一個直角三角形?如果是的話,是不是直角三角形的三邊長都會有 a平方+b平方=c平方的關係存在?
我們還討論了歸納法和演繹法,男人是人,人不一定是男人的邏輯問題。因為 3-4-5是一個特例,從特例出發只能算是推論、猜測,還需要證明。
我們一起看了一個影片巧手摺紙學數學--摺紙證明畢氏定理(方法2) - YouTube ,非常高明,兒子看了好驚訝,我們也嘗試著自己摺紙看看,也畫畫看。雖然很佩服,但我覺得這種證明法似乎還是很難「想」得出來。
後來我又找到一個影片,小學生都識證明畢氏定理 - YouTube 粵語發音雖然聽不太懂,但看得懂操作過程,很棒的證明,更簡單更容易理解!
我興緻勃勃的去找兒子,但我沒發現他已經被我燒腦過度已經開始不耐煩了,但他還是很乖的照我的要求,用厚紙板剪了八個直角三角形,兩股分別是3公分和7公分。
我畫了兩個邊長為10公分的正方形,要兒子試試看能不能用這個來證明畢氏定理。但兒子已經想去做自己想做的事了,我還自己在那邊一頭熱的要燒他的腦袋,他跟我說他看不懂想不出來不想做。
女兒在一旁則是很有興趣的過來排排看,兒子逃走了。唉!是我的問題,我覺得很好玩,兒子未必覺得好玩,尤其是在他想休息做別的事的時候。
我在看過畢氏定理的引入 | 畢氏定理 | 均一教育平台 後,覺得「畢氏定理」作為代數和幾何的橋樑,非常適合做為在我家私塾時間探索的開頭。我跟兒子說「平方」讓人想到的第一件事情就是正方形面積,我要兒子剪三個正方形。
做好之後,兒子很自然地就把三個正方形排成上圖的樣子,我很驚訝地問他為什麼要這樣排?他笑說之前他有看到我在看數學影片時,我叫他不要看我要鋪梗,雖然他只看了一眼但已經記住那個排法了。哈哈,本來是要給他看倒水的影片,後來忘記給他看了。
我問兒子說你覺得那三個正方形圍起來的三角形,會不會是一個直角三角形?如果是的話,是不是直角三角形的三邊長都會有 a平方+b平方=c平方的關係存在?
我們還討論了歸納法和演繹法,男人是人,人不一定是男人的邏輯問題。因為 3-4-5是一個特例,從特例出發只能算是推論、猜測,還需要證明。
我們一起看了一個影片巧手摺紙學數學--摺紙證明畢氏定理(方法2) - YouTube ,非常高明,兒子看了好驚訝,我們也嘗試著自己摺紙看看,也畫畫看。雖然很佩服,但我覺得這種證明法似乎還是很難「想」得出來。
後來我又找到一個影片,小學生都識證明畢氏定理 - YouTube 粵語發音雖然聽不太懂,但看得懂操作過程,很棒的證明,更簡單更容易理解!
我興緻勃勃的去找兒子,但我沒發現他已經被我燒腦過度已經開始不耐煩了,但他還是很乖的照我的要求,用厚紙板剪了八個直角三角形,兩股分別是3公分和7公分。
我畫了兩個邊長為10公分的正方形,要兒子試試看能不能用這個來證明畢氏定理。但兒子已經想去做自己想做的事了,我還自己在那邊一頭熱的要燒他的腦袋,他跟我說他看不懂想不出來不想做。
女兒在一旁則是很有興趣的過來排排看,兒子逃走了。唉!是我的問題,我覺得很好玩,兒子未必覺得好玩,尤其是在他想休息做別的事的時候。






留言